Boggle Solver
The game of Boggle is a relatively simple game where players try finding words in an \(n \times n\) board of letters. Words are constructed by following a simple path of adjacent letters on the board, i.e. a path where each letter is visited at most once. In the below example, the word ‘BOGGLE’ itself is found on the Boggle board. See if you can also find the words TURD, BRIDGE, GIRDLE, TOGGLED, STRIDE, and GUIDE. There are many more possible words on the board.
 Source: Google images
Source: Google images
Players individually try finding as many words as they can under a time limit. After the time limit, they compare how many words they found, with longer words counting as more points, and the player with the most points wins.
In this blog, I’ll work you through my brief history with this game, my computer implementation(s), and an attempt of asymptotic analysis of these implementations.
My History with Boggle #
In early 2018, I played Boggle with my friend online on this website. My friend handily beat me every time. Perhaps it is more accurate to say crushed me. Needless to say the outcome was unacceptable. So I made them a bet that within the span of one day I would be able to consistently beat them. They naively took the bet. My grandfather taught me that there are exactly two people in every bet—the cheater and the idiot. If you’re not the cheater, then you’re the idiot.
So I practiced my C++ coding (the language I had just started learning at the time) to solve the game of Boggle, and use it to win every game. All I had to do was tell it what letters were showing on the board, and the program handle the rest, typing in all the words for me at a far faster rate than I could ever emulate.
After challenging them again, my friend very quickly realized what I had done, found it very amusing, and conceded the bet. As a side note, the other players on the website were a lot less amused, calling me a ‘cheat’, and getting very annoyed. This confused me, as my high scores were not negatively affecting their scores / ratings in any way. Furthermore, the attitude of this site creator didn’t leave me any room for sympathy, see the image below taken from the site forum. Note that this snapshot was taken in late 2021, over three and a half years after this incident.
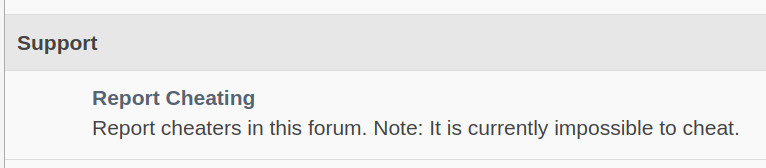
Unfortunately, shortly after this incident, my laptop was stolen, before I had a chance to upload my program to version control. That was especially unfortunate since three and a half years later, another friend started handily beating me in online Boggle… Let’s just say I chose not to be the idiot again. This time, my code is on GitHub. Fun side note: I wrote this program with the help of GitHub Copilot, which was pretty helpful, and probably reduced ~10-20% of the total programming time.
My Computer Implementations #
I remember my first implementation was relatively efficient, but it is lost to history now. I don’t remember it well enough though, so it is effectively lost to time. I imagine it is relatively similar to my current algorithm, which is the one I’ll describe below:
My algorithm works by iterating over the dictionary word by word and checking whether it can be found in the Boggle board. Checking whether it can be found in the board can be done by iterating letter by letter and seeing if the next letter can be found in any adjacent square. If this can be done for all the letters in the word and no letter was visited twice, then the word can be found. For example, consider the below animation where the word SOGGED is searched for on the board:

For those of you familiar with computer science problems, this can be easily implemented using a depth-first search algorithm. See the Wikipedia article if you are not familiar. My algorithm worked as follows:
- For each letter, a list of squares containing that letter is made
- For each word, iterate over these initial squares
- For each of the initial squares, initiate a depth-first search traversal where squares are recursed into when they satisfy the following conditions:
- are adjacent to the previous node (8 adjacent squares)
- are within the bounds of the board
- have not yet been visited on the path
- contain the same letter as the next letter in the word
An algorithm implementing the above was plenty fast enough for the purposes of this problem. It is worth noting that in Boggle, traditionally there is no ‘Q’ square, rather than a ‘Qu’ square. Modifying the above algorithm to handle ‘Q’s correctly is trivial, and is left as an exercise for the reader (or just check out my code on GitHub).
Mathematical Analysis #
This algorithm was designed with coding speed efficiency in mind rather than coding performance efficiency in mind. I needed to program something within a few hours, and execution time was not a bottleneck. That being said, why not try analyzing the performance of the program?
Worst-Case Analysis #
First, we can see that for this algorithm in the worst case, a single word can run in exponential time. One way of thinking about it is considering the following case: the board is composed of all the same letter, say ‘A’, and the word searched for contains all ‘A’s except one ‘B’ at the end. For example, imagine searching for the word AAAAAAAAAAAAAAAB (15 A’s and 1 B) in the board represented below:
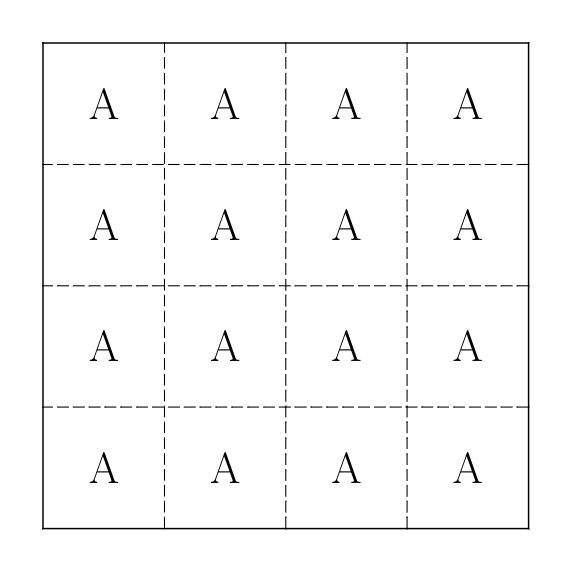
Every single simple directed path in this graph will be traversed when trying to find the word. Let’s consider our algorithm to upper-bound the total amount of times a node will be visited.
- every single square will be tried out as a starting square, which is \(l \times w\) squares
- for every character in the word, there will be at most 8 directions checked and recursed into
- the recursion will happen at most once for each letter minus one (the minus one is due to the first letter)
So we get a very rough upper bound of \(O(l w \cdot 8^{l w - 1})\), which is clearly exponential bound. We can improve this bound by seeing that for every recursive iteration except the first iteration, there can actually only be 7 viable directions (since the previous location was already visited), so we get \(O(l w \cdot 7^{l w - 1})\).
The base of the exponent can also be reduced since the boundaries of the board have fewer viable adjacent squares, although as the length and width of the board become arbitrarily large, the fraction of border squares becomes arbitrarily small. Another observation is as the traversal continues, more and more squares become visited, meaning there are fewer and fewer viable squares. In fact, some paths may end up in dead-ends and have 0 adjacent vertices. It is not yet clear what the average branching factor (number of viable adjacent squares in any given state) is.
We can make one potentially helpful observation by recalling that the number of times each node will be visited, which is proportional to the running time of our algorithm, is equivalent to the number of simple directed paths in the graph. A graph with edges identical to those of the Boggle board is called a King’s graph. A King’s graph is a graph where the edges represent all the moves a chess King can make, see the image below:

I calculated the total number of these paths for various board sizes, and plotted my results in the appendix below. While for \(n \times 1\) graphs there are only \(n^2\) simple directed paths, for \(n \times n\) graphs there are many more, see OEIS A236690. Trying to best-fit \(n^2 b^{n^2}\) to the first 10 values of this sequence, we get a value of \(b\) that seems to be approaching Euler’s constant, \(e\). This constant appears in many similar areas of mathematics, so I conjecture that for this \(n \times n\) case, the number of simple directed paths is \(\Theta( n^2 e^{n^2} )\) or equivalently \(\Theta(v e^v)\) where \(v\) is the number of vertices. I further conjecture that for any fixed width graph \(n \times w\), the number of simple directed paths is \(\Theta(n^2 b^{n^2})\), where \(b\) monotonically increases from \(1\) to \(e\). Note that for the aforementioned \(n \times 1\) case, the branching factor \(b\) would be \(1\). Also note the similarity between this bound and the one we thought through above. Please contact me if you discover anything.
We’ve started to gain confidence that the worst case time complexity for a single word is exponential time, that is clearly not the average case bound.
Another Simple Analysis #
On the other end of the spectrum, we can make a lot of simplifying assumptions. The size of the board does not change from game to game. In classic Boggle, the board is always \(4 \times 4\). The largest board on the aforementioned website is \(8 \times 8\). For all practical purposes, the board size is bounded. And if the board size is bounded, then the total number of simple directed paths is also bounded. Therefore we can justify the claim that the algorithm runs in \(\Theta(1)\) time per word. This analysis, however, is not meaningful, as nearly any algorithm could use the same logic and get the same time bound.
Average-Case Analysis Attempt #
Average-case analyses are generally hard to do, but we will attempt one regardless. Let us assume a uniform distribution of letters over the board. Furthermore, let us assume that each letter in a given word is picked independently over a uniform distribution of the letters in the English alphabet. The average number of locations that the letter can start in, then, is the total number of squares times the likelihood of each letter (\(\frac{1}{26}\)), so:
\begin{equation} \text{# squares at depth 0 } = \frac{l \cdot w}{26} \end{equation}
where \(l\) is the board length, \(w\) is the board width, and 26 is the number of letters in the (English) alphabet.
From this first step of the analysis, we already have a lower bound for the performance of this algorithm: \(\Omega(l \cdot w)\).
The average number of squares that would be visited for the second letter is the total number of squares from the first letter times the average number of adjacent squares that would contain the second letter. The average number of adjacent squares that contain the second letter is the branching factor (which is bounded by 8), again times the likelihood of each letter:
\begin{equation} \text{# squares at depth 1 } \leq \frac{l \cdot w}{26} \left (\frac{8}{26} \right ) \end{equation}
At each depth, the average number of squares traversed at the next depth is the average from the previous depth times the number of adjacent squares, so we obtain the following general equation:
\begin{equation} \text{# squares at depth } d \leq \frac{l \cdot w}{26} \left (\frac{8}{26} \right )^d \end{equation}
With this in mind, the total number of squares traversed is:
\begin{equation} \text{total # squares traversed } \leq \sum_{d = 0}^\text{# letters in word}{\frac{l \cdot w}{26} \left (\frac{8}{26} \right )^d} \end{equation}
The total number of letters in the word is finite, so we can say:
\begin{equation} \text{total # squares traversed } \leq \sum_{d = 0}^\infty{\frac{l \cdot w}{26} \left (\frac{8}{26} \right )^d} \end{equation}
Finally, the equation of the sum of a geometric series can be used to show:
\begin{equation} \text{total # squares traversed } \leq \frac{l \cdot w}{26 - 8} = \frac{l \cdot w}{18} \end{equation}
Note that all the above equations are only for the average-case analysis as defined above.
From the final step of this analysis, we get the convenient solution that each word takes \(O(l \cdot w)\) time. Since this is identical to the lower bound we already found, we can make the stronger claim that this algorithm runs in \(\Theta(l \cdot w)\) in the average case (as defined above).
While this analysis found the average performance of this algorithm, it made no attempts to find the variance of this average. This is left as an exercise for the readers.
Conclusion #
It is relatively very easy to solve the game of Boggle in linear time (relative to the number of squares), in the average case. The analysis for the worst-case time is unresolved, and I’d be curious to hear any developments on that front. And, most importantly, never agree to weird bets unless you plan on cheating :)
Appendix #
Table 1: Number of simple directed paths on an \(l \times w\) king graph #
| length | width | num paths |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 4 |
| 2 | 2 | 64 |
| 3 | 1 | 9 |
| 3 | 2 | 476 |
| 3 | 3 | 10305 |
| 4 | 1 | 16 |
| 4 | 2 | 2904 |
| 4 | 3 | 193924 |
| 4 | 4 | 12029640 |
| 5 | 1 | 25 |
| 5 | 2 | 15828 |
| 5 | 3 | 3244045 |
| 5 | 4 | 659935616 |
| 5 | 5 | 115066382913 |
| 6 | 1 | 36 |
| 6 | 2 | 81360 |
| 6 | 3 | 50563268 |
| 6 | 4 | 33995987408 |
Table 2: Number of simple directed paths on an \(l \times 2\) king graph #
| length | num paths |
|---|---|
| 2 | 64 |
| 3 | 476 |
| 4 | 2904 |
| 5 | 15828 |
| 6 | 81360 |
| 7 | 405452 |
| 8 | 1988552 |
| 9 | 9674692 |
| 10 | 46882752 |
| 11 | 226754492 |
| 12 | 1095729080 |
| 13 | 5292556212 |
| 14 | 25558908848 |
| 15 | 123418443692 |
| 16 | 595936673704 |
Table 3: Number of simple directed paths on an \(l \times 3\) king graph #
| length | num paths |
|---|---|
| 3 | 10305 |
| 4 | 193924 |
| 5 | 3244045 |
| 6 | 50563268 |
| 7 | 750683101 |
| 8 | 10768467844 |
| 9 | 150643844893 |
Table 4: Number of simple directed paths on an \(l \times 4\) king graph #
| length | num paths |
|---|---|
| 4 | 12029640 |
| 5 | 659935616 |
| 6 | 33995987408 |
| 7 | 1669552434996 |